Simplifying a Polyline - The Implementation
The following implementation assumes we have an array of points named points. This array's indices range in the closed interval from 0 to n-1 where n is the length of the array.
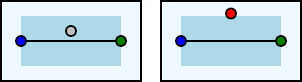
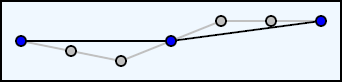
As defined in the previous section, tolerance specifies the minimum distance a point must stray from a line before it is no longer considered a part of the line. The following diagram helps to demonstrate this point.
As can be seen from the left side of the diagram, the grey circle is not on the line, but it is inside the light blue region that indicates the current tolerance; therefore, we consider that point to be on the line. The right side of the diagram shows that the middle point is outside of the tolerance region and is therefore considered to be off of the line.
Before proceeding, I should describe the conventions I am using in the diagrams in this section.
- A blue circle indicates a point in the polyline that has been determined to be a vertex in the resulting polyline. The last blue circle in a polyline is known as the "last accepted point"
- Grey circles indicate a point that has been determined to be on the polyline within the given tolerance value
- A green circle indicates the current point that is being tested
- A red circle indicates a point that has been determined not to be on the polyline given the tolerance value
- The current line being tested is the line from the last blue circle to the green circle. This is referred to as the "current line"
- The light blue rectangle around the current line visualizes the area considered to be on the line given the tolerance value. This area is referred to as the "tolerance region"
- Although not shown here, later diagrams will include white circles which indicate points in the original polyline that have not yet been visited by the algorithm
You may want to note that for a point to be considered inside of the tolerance region, the circle's center must be on the border or within the tolerance region. You may have noticed that the red circle is touching the tolerance region, but the center point is outside of the region and therefore it is considered to be outside of the tolerance region.
The purpose of this algorithm is to remove points from the original polyline while preserving its appearance as compared to the original polyline. In order to remove points, we need to consider at least three points in the original curve. A single point does not define a line, so it is meaningless to determine if that point by itself is on a line. Two points define a line; therefore, both are on the line and can never be outside any given tolerance. Having three points is the first case where we can determine if a point is within a tolerance.
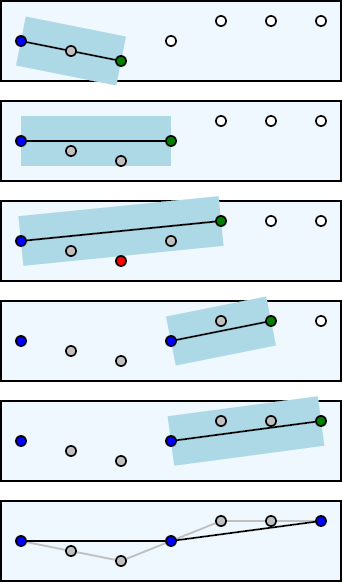
In order to get things started in the algorithm, we need to prime the algorithm's pump, so to speak. We need three points to begin eliminating points. The first point of the polyline cannot be eliminated as discussed above, so we add that point to our result array. The second point could possibly be eliminated, but we cannot test it for elimination unless we use the first and third points as our test line. Therefore, we prime the pump by defining the last accepted point as points[0] and we define the current test point as points[2].
A series of diagrams will follow showing each step in the algorithm so we can get a feel of what the algorithm is doing along the way.
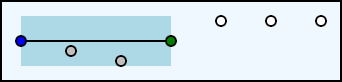
Now that we have initialized the algorithm, we can begin looping through the remaining points in the original polyline data, removing points outside of the tolerance for each line being tested. The first test will be to determine if points[1] is within tolerance of the line defined by the last accepted point (points[0]) and the current point (points[2]).
As we can see, the test line is defined by the last accepted point (the blue circle) and the current point (the green circle). The second point (the grey circle) was tested and was determine to be within the tolerance region (the light blue rectangle). Since that point is in the tolerance region, we advance to the next point in the original polyline data.
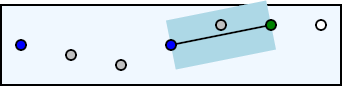
Again, we create a line from the last accepted point (the blue circle) to the current point (the green circle). These two points define a new line, so we must test all points between the end points of the line to determine if any of the interior points fall outside of the tolerance region. If any of those points do fall outside that region, then the current line does not approximate the original polyline within tolerance.
As we can see in the previous image, the second and third points are still within the tolerance region, so we proceed to the next point in the original polyline data.
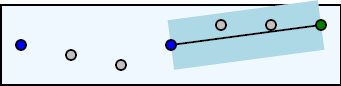
This is the first instance where we have found a point (the red circle) outside of the tolerance region. This means that we cannot approximate the original polyline within the user-specified tolerance by drawing a line from the last accepted point (the blue circle) to the current point (the green circle). However, the point before the current point did not result in any of the test points falling outside of the tolerance region, so we can define that previous point to be an accepted point. We add that point to our result array which means that it is now the last accepted point and then we continue processing with the point following the current point.
As can be seen by the next diagram, this leaves us in the perfect state to continue processing. The last accepted point and the new current point result in one inner point, or three points as needed by the algorithm. This is the same state we needed to initialize the algorithm. In other words, we don't need to do anything special to make sure that we have enough points to continue.
In the above image, we find that the inner point is within tolerance, so we advance to the next point.
Once again, all inner points are within tolerance, so we advance to the next point, but there is no next point. As it turns out, it is impossible for the last point ever to become a last accepted point. A last accepted point is always the point before the current point. Since there are no points following the last point, it can never be the point before the current point. All of this is to say that our algorithm will always end by adding the last point of the original polyline data to our result array.
The algorithm has completed.
The next diagram shows the points from the original polyline and the polyline itself (the grey line). The blue points show the points that were within tolerance and as consequence were added to the result array. Then we show the simplified polyline (the black line) so we can compare its appearance to the original polyline. Note that our scale is exaggerated for easier viewing. In real life, the differences between the two polylines will be much less noticeable unless, of course, you use a very large tolerance value.
Oftentimes, I find it easier to understand algorithms visually than through prose. I think this is particularly true when one is learning an algorithm that is visual in nature to begin with. The image below collects all the steps described above into one image for the convenience of those who prefer diagrams to prose.
I discovered one problem that occurs when the user draws a sharp corner. When you draw a corner, you end up with a number of points that are close together. This probably has something to do with the fact that you have to decelerate to a full stop in one direction and then accelerate in a new direction. This coupled with the sampling rate of the mousemove events results in a cluster of points. A "corner" in the hand-drawn curve might look like the following image.
We end up losing the sharp corner because the points are so close together. As can be seen in the next diagram, the mid-point that creates the corner falls inside of the tolerance. As a result, the corner will be removed which will cause the resulting polyline to look noticeably different than the original.
To get around this situation, we need to identify sharp corners. When we encounter a point that creates a corner we consider that point to be an accepted point. Accepted points are added to the result array and become the last accepted point.
I decided to classify a point as a corner point if the angle it creates with the previous and following points is less than or equal to 90 degrees. This has worked well for me, but you may want to fine tune the "corner" angle, if you are not happy with the results.